Desvendando o Poder das Transformações Matriciais e Sistemas de Coordenadas com Python

​Durante minha caminhada em projetar UAVs, UGVs e alguns poucos USVs, para atuar em operações de vigilancia da amazônia, dominar Transformações de Matrizes e Sistemas de Coordenadas, foi uma habilidade essencial que precisei adquiri. E implementa-las com Python para Computação Gráfica, levou os projetos além de uma simples maquina de monitoramento e inspeção. ​ No dinâmico e fascinante campo da visão computacional e da computação gráfica, a capacidade de manipular e interpretar dados espaciais é fundamental. ​Seja para renderizar mundos virtuais imersivos em jogos de última geração, desenvolver sistemas de realidade aumentada que sobrepõem informações digitais ao nosso entorno, ou até mesmo para guiar veículos autônomos com precisão milimétrica, o domínio sobre as transformações de matrizes e os sistemas de coordenadas se revela como uma habilidade indispensável. Este artigo propõe uma jornada profunda por esses conceitos, desmistificando a matemática por trás da projeção de objetos tridimensionais em imagens bidimensionais e explorando como essa poderosa ferramenta nos permite, por exemplo, "travar" em um alvo específico e manter uma perspectiva orbital constante em cenários complexos.

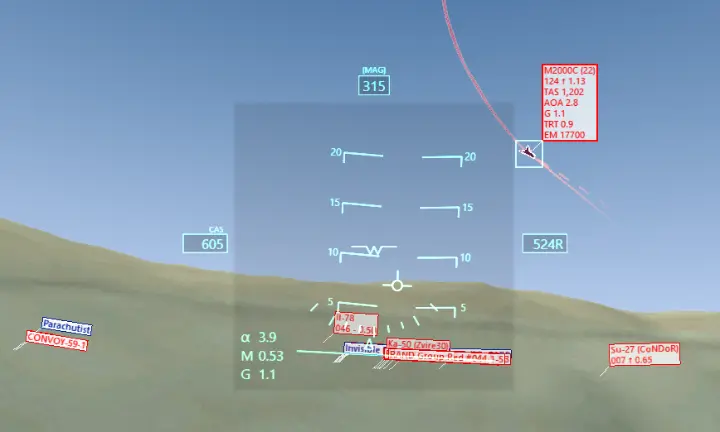
​Imagine a cena: um piloto de dronehabilidoso, no comando de uma aeronave de alta performance, precisa identificar e acompanhar um alvo em movimento rápido. ​A tela à sua frente, o Head-Up Display (HUD), traduz um fluxo contínuo de dados tridimensionais do ambiente em informações visuais claras e acionáveis. ​Essa "mágica" acontece graças a uma série de cálculos precisos, onde as coordenadas do mundo real são transformadas, passo a passo, até se tornarem pixels na tela do piloto. Abordaremos não apenas a teoria por trás dessas transformações, mas também como implementá-las de forma prática, utilizando a linguagem Python para dar vida a esses conceitos. ​Prepare-se para desvendar como a álgebra linear se torna a espinha dorsal de sistemas que interagem com o espaço, desde a simples exibição de um objeto 3D em seu monitor até a complexa tarefa de manter um "lock-on" persistente em um ponto de interesse, mesmo enquanto a câmera (ou o observador) se move e rotaciona pelo ambiente.

A Dança das Matrizes: Transformações Fundamentais

​Agora que estabelecemos os diferentes palcos (sistemas de coordenadas), é hora de entender como os atores (nossos objetos 3D) se movem e se transformam dentro deles e entre eles. A linguagem universal para descrever essas transformações no mundo da computação gráfica é a álgebra linear, e as matrizes são suas protagonistas. Elas nos permitem codificar e aplicar transformações como translação, rotação e escala de forma elegante e eficiente.

Translação: Movendo pelo Espaço

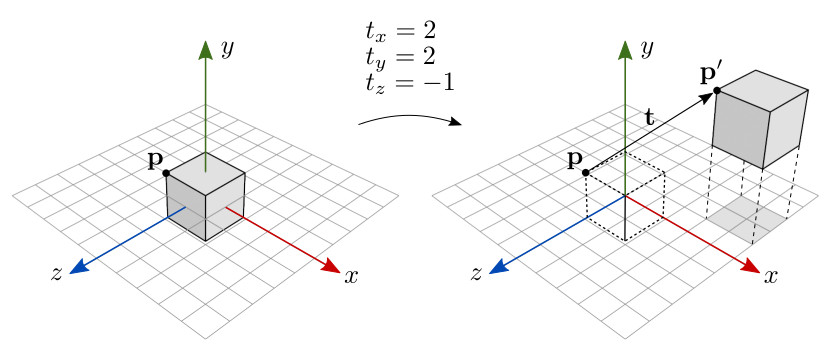
​A translação é a mais simples das transformações: ela simplesmente move um objeto de um ponto a outro, sem alterar sua orientação ou tamanho. Imagine pegar uma maçã em sua mesa e movê-la para a direita; isso é uma translação. Em termos matemáticos, se um ponto P tem coordenadas (x, y, z), uma translação por um vetor T = (tx, ty, tz) resultará em um novo ponto P' com coordenadas (x+tx, y+ty, z+tz).

Rotação: Girando em Torno de um Eixo

​A rotação descreve o movimento de um objeto em torno de um eixo fixo. Pense em um pião girando em torno de seu eixo central, ou a Terra girando em torno de seu eixo polar. ​A rotação é definida por um eixo de rotação e um ângulo. Implementar rotações pode ser um pouco mais complexo, envolvendo senos e cossenos, mas a ideia central é mudar a orientação do objeto sem alterar sua posição relativa ao eixo de rotação (a menos que o eixo não passe pela origem do objeto, o que introduziria uma translação também).

Escala: Aumentando ou Diminuindo

​A escala altera o tamanho de um objeto. Podemos aumentar ou diminuir o objeto uniformemente em todas as direções (como inflar um balão) ou de forma não uniforme, esticando ou comprimindo-o ao longo de eixos específicos (como transformar uma bola de basquete em uma bola de futebol americano).

Cisalhamento (Shearing): Distorcendo com Estilo

​Menos comum no dia a dia, mas importante em computação gráfica, o cisalhamento é uma transformação que inclina o objeto. Imagine empurrar o topo de um baralho de cartas para o lado enquanto a base permanece fixa; as cartas deslizam umas sobre as outras, criando uma forma distorcida. Essa é a essência do cisalhamento.

Combinando Transformações: A Mágica das Matrizes de Transformação

​A verdadeira força das matrizes reside na sua capacidade de combinar múltiplas transformações em uma única operação. Em vez de aplicar uma translação, depois uma rotação e depois uma escala separadamente, podemos multiplicar suas respectivas matrizes para obter uma única matriz de transformação que realiza todas essas operações de uma vez. Isso é incrivelmente eficiente e fundamental para a renderização em tempo real em jogos e simulações.

​Por exemplo, para posicionar um objeto em uma cena, normalmente começamos com o objeto em sua própria origem (coordenadas locais). Em seguida, aplicamos uma série de transformações:

1. Escala: Para ajustar o tamanho do objeto.
2. Rotação: Para orientar o objeto corretamente.
3. Translação: Para mover o objeto para sua posição final no mundo.

​Essas transformações são frequentemente combinadas em uma única matriz conhecida como Matriz de Modelo (Model Matrix). Essa matriz transforma os vértices do objeto de seu espaço local para o espaço do mundo.

​Posteriormente, como vimos, a Matriz de Visualização (View Matrix) transforma as coordenadas do espaço do mundo para o espaço da câmera, e a Matriz de Projeção (Projection Matrix) mapeia as coordenadas da câmera para o espaço de recorte, que é então mapeado para a tela.

Foco no Alvo: Implementando o "Lock-On" Conceitual

​Um dos aspectos mais dinâmicos e visualmente interessantes na computação gráfica e em simulações interativas é a capacidade de uma câmera (ou de um observador virtual) manter seu foco fixo em um objeto específico, independentemente de como a câmera ou o objeto se movem. Esse conceito, popularmente conhecido como "lock-on" ou "target tracking", é fundamental em jogos, sistemas de vigilância, robótica e muitas outras aplicações. A ideia é simples: não importa para onde a câmera se desloque ou como ela rotacione em seus próprios eixos, sua "atenção" deve permanecer direcionada para o alvo.

O Desafio da Perspectiva Dinâmica

​Imagine que você está controlando uma câmera em um ambiente 3D e deseja que ela sempre olhe para um carro em movimento. Se a câmera estiver parada e o carro se mover, a câmera precisa girar para acompanhar o carro. Se o carro estiver parado e a câmera se mover ao redor dele, a câmera precisa ajustar sua orientação continuamente para manter o carro no centro de sua visão. Se ambos estiverem se movendo, a complexidade aumenta, mas o princípio permanece o mesmo: a direção "para frente" da câmera deve sempre apontar da posição da câmera para a posição do alvo.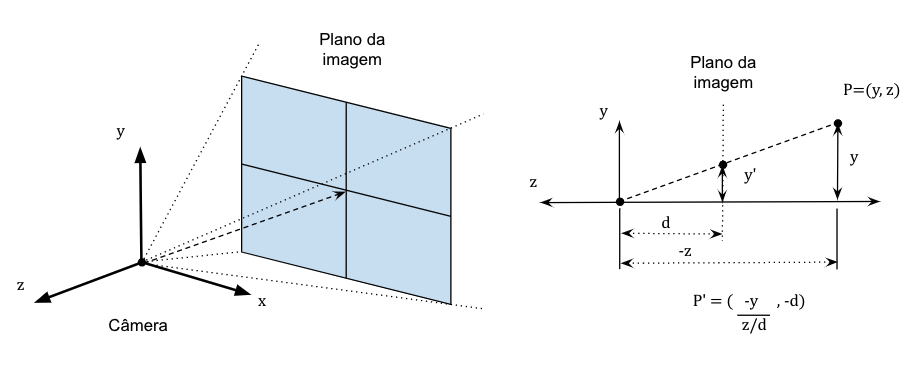

A Matemática por Trás do Olhar Fixo

Para implementar um sistema de "lock-on", precisamos, a cada quadro ou atualização de cena, recalcular a orientação da câmera. O processo conceitual envolve os seguintes passos:

1. Identificar Posições: Precisamos conhecer a posição atual da câmera no Sistema de Coordenadas do Mundo (vamos chamá-la de posicao_camera) e a posição atual do alvo no mesmo sistema (vamos chamá-la de posicao_alvo).
2. Calcular o Vetor Direção: Com essas duas posições, podemos calcular um vetor que aponta da câmera para o alvo. Esse vetor, que chamaremos de vetor_direcao_alvo, é simplesmente posicao_alvo - posicao_camera. Este vetor nos dá a linha de visão desejada.
3. Definir a Orientação da Câmera: O desafio agora é alinhar o eixo "para frente" da câmera (geralmente o eixo Z local da câmera) com este vetor_direcao_alvo. No entanto, apenas definir a direção "para frente" não é suficiente para determinar completamente a orientação da câmera. Uma câmera pode estar olhando para um ponto, mas ainda pode girar em torno do eixo que aponta para esse ponto (como inclinar a cabeça enquanto olha para algo). Precisamos de mais uma referência para estabilizar a câmera, geralmente um vetor "para cima" (up vector).
4. O Vetor "Para Cima" (Up Vector): Um vetor "para cima" global (por exemplo, o eixo Y positivo do Sistema de Coordenadas do Mundo, (0, 1, 0)) é frequentemente usado como uma referência inicial. Este vetor ajuda a definir qual direção é "para cima" para a câmera, evitando que ela role descontroladamente.
5. Construindo a Matriz de Visualização (View Matrix): Com o vetor_direcao_alvo (que se tornará o novo eixo Z negativo da câmera, após normalização) e o vetor "para cima" de referência, podemos usar produtos vetoriais para construir os outros dois eixos ortogonais da câmera:
   • O novo eixo X da câmera (direita) pode ser calculado como o produto vetorial normalizado entre o vetor "para cima" de referência e o vetor_direcao_alvo.
   • O novo eixo Y da câmera (para cima real) pode ser calculado como o produto vetorial normalizado entre o vetor_direcao_alvo e o novo eixo X da câmera.
   Esses três vetores ortonormais (direção, direita, cima), juntamente com a posição da câmera, definem completamente a orientação e a posição da câmera no espaço. Eles podem ser usados para construir diretamente a Matriz de Visualização. Muitas bibliotecas gráficas fornecem funções como lookAt(posicao_camera, posicao_alvo, vetor_up_referencia) que realizam esses cálculos internamente e retornam a Matriz de Visualização resultante.

Considerações Importantes:

• Singularidades: Se o vetor_direcao_alvo e o vetor "para cima" de referência se alinharem (por exemplo, se a câmera estiver olhando diretamente para cima ou para baixo em relação ao vetor "para cima" de referência), o produto vetorial para calcular o eixo X pode resultar em um vetor nulo, causando problemas. Implementações robustas precisam lidar com esses casos de singularidade, geralmente escolhendo um vetor "para cima" de referência alternativo temporariamente.
• Suavização: Em aplicações em tempo real, mudanças abruptas na orientação da câmera podem ser desconfortáveis. Frequentemente, técnicas de interpolação ou suavização (como Slerp para quaterniões, que são outra forma de representar rotações) são usadas para fazer a câmera girar suavemente em direção ao alvo, em vez de "pular" instantaneamente para a nova orientação.

Este mecanismo de "lock-on" é uma aplicação direta da manipulação de vetores e da construção de matrizes de transformação. Ele transforma um problema de manter o foco visual em uma série de operações geométricas bem definidas, permitindo que a câmera siga dinamicamente seu ponto de interesse através do espaço tridimensional. Na seção de implementação com Python, veremos como traduzir esses conceitos em código funcional.

Orbitando o Ponto de Interesse: Mantendo a Perspectiva

Uma vez que conseguimos "travar" a câmera em um alvo, o próximo passo lógico é permitir que ela orbite em torno desse ponto de interesse. Imagine um satélite girando em torno da Terra, ou uma câmera de segurança que precisa monitorar um objeto de todos os ângulos. Essa funcionalidade é crucial em muitas aplicações, desde a visualização de modelos 3D até a criação de cenas cinematográficas em jogos.

A Mecânica da Órbita:

Para implementar uma câmera orbital, precisamos definir alguns parâmetros chave:

1. Ponto de Foco (Target): O objeto ou ponto no espaço ao redor do qual a câmera irá orbitar. Este é o mesmo target_position que usamos para o "lock-on".
2. Distância: A distância constante que a câmera manterá do ponto de foco durante a órbita.
3. Ângulos de Rotação: Precisamos de pelo menos dois ângulos para definir a posição da câmera na esfera imaginária ao redor do alvo:
   • Azimute (Yaw): A rotação horizontal da câmera em torno do alvo.
   • Elevação (Pitch): A rotação vertical da câmera, olhando para cima ou para baixo em direção ao alvo.
     
     

Um breve conceito de exemplo para Implementação em Python (Conceitual):

import math

# Posição do alvo (exemplo)
target_position = [0, 0, 0]  # Em coordenadas do mundo

# Parâmetros da órbita
distance = 10.0  # Distância da câmera ao alvo
azimuth_angle = math.radians(45)  # Ângulo de azimute em radianos
elevation_angle = math.radians(30)  # Ângulo de elevação em radianos

# Calcular a posição da câmera
camera_x = target_position[0] + distance * math.cos(elevation_angle) * math.sin(azimuth_angle)
camera_y = target_position[1] + distance * math.sin(elevation_angle)
camera_z = target_position[2] + distance * math.cos(elevation_angle) * math.cos(azimuth_angle)

camera_position = [camera_x, camera_y, camera_z]

print(f"Posição da Câmera: {camera_position}")

Observações Importantes:

• Sistema de Coordenadas: É crucial que todas as posições (alvo, câmera) estejam no mesmo sistema de coordenadas (geralmente, o Sistema de Coordenadas do Mundo).
• Controles do Usuário: Em uma aplicação interativa, você normalmente permitiria que o usuário controlasse os ângulos de azimute e elevação, bem como a distância, através do mouse ou teclado. Isso permitiria ao usuário girar a câmera ao redor do alvo e aproximar/afastar a visão.
• Limites e Restrições: Em algumas situações, pode ser necessário restringir os ângulos de elevação para evitar que a câmera "vire de cabeça para baixo" ou passe por baixo do "chão" da cena. Isso pode ser feito limitando os valores dos ângulos de elevação (por exemplo, entre -89 graus e +89 graus).
• Suavização: Para movimentos de câmera mais suaves e cinematográficos, em vez de atualizar a posição da câmera instantaneamente, você pode interpolar suavemente entre a posição antiga e a nova posição ao longo de vários frames.

​Dominar a órbita da câmera é essencial para criar experiências interativas e visuais envolventes, permitindo que os usuários explorem cenas 3D de forma intuitiva e eficaz. Combinado com o "lock-on", isso cria um sistema de câmera poderoso e versátil.

Python em Ação: Exemplos Práticos e Visualizações

​Agora que exploramos os conceitos teóricos das transformações de matrizes, sistemas de coordenadas, "lock-on" e câmeras orbitais, é hora de colocar a mão na massa com Python. Utilizaremos a biblioteca NumPy para as operações matriciais, dada sua eficiência e conveniência para cálculos numéricos. Para visualizações, embora uma biblioteca gráfica completa como PyOpenGL ou Pygame fosse ideal para uma demonstração interativa, focaremos nos cálculos principais que podem ser integrados a qualquer motor gráfico.

Configuração Inicial e Matrizes Básicas

Primeiro, certifique-se de ter o NumPy instalado (´pip install numpy´).

import numpy as np
import math

def criar_matriz_translacao(tx, ty, tz):
    return np.array([
        [1, 0, 0, tx],
        [0, 1, 0, ty],
        [0, 0, 1, tz],
        [0, 0, 0, 1]
    ])

def criar_matriz_escala(sx, sy, sz):
    return np.array([
        [sx, 0, 0, 0],
        [0, sy, 0, 0],
        [0, 0, sz, 0],
        [0, 0, 0, 1]
    ])

def criar_matriz_rotacao_x(angulo_rad):
    c = np.cos(angulo_rad)
    s = np.sin(angulo_rad)
    return np.array([
        [1, 0, 0, 0],
        [0, c, -s, 0],
        [0, s, c, 0],
        [0, 0, 0, 1]
    ])

def criar_matriz_rotacao_y(angulo_rad):
    c = np.cos(angulo_rad)
    s = np.sin(angulo_rad)
    return np.array([
        [c, 0, s, 0],
        [0, 1, 0, 0],
        [-s, 0, c, 0],
        [0, 0, 0, 1]
    ])

def criar_matriz_rotacao_z(angulo_rad):
    c = np.cos(angulo_rad)
    s = np.sin(angulo_rad)
    return np.array([
        [c, -s, 0, 0],
        [s, c, 0, 0],
        [0, 0, 1, 0],
        [0, 0, 0, 1]
    ])

Implementando a Câmera "Look-At" (Lock-On)

Conforme discutido, a função look_at é fundamental para direcionar a câmera.

def normalizar_vetor(vetor):
    norma = np.linalg.norm(vetor)
    if norma == 0:
        return vetor
    return vetor / norma

def look_at(posicao_camera, posicao_alvo, vetor_up_mundo):
    # Eixo Z da câmera (direção oposta à visão, aponta para longe do alvo)
    z_cam = normalizar_vetor(posicao_camera - posicao_alvo)
    # Eixo X da câmera (produto vetorial do "up" do mundo com Z da câmera)
    x_cam = normalizar_vetor(np.cross(vetor_up_mundo, z_cam))
    # Eixo Y da câmera (produto vetorial de Z e X da câmera)
    y_cam = normalizar_vetor(np.cross(z_cam, x_cam))

    # Matriz de Rotação Inversa (da câmera para o mundo)
    # Para a matriz de visualização, queremos do mundo para a câmera, então usamos a transposta
    # dos eixos da câmera, pois eles formam uma base ortonormal.
    matriz_rotacao = np.array([
        [x_cam[0], x_cam[1], x_cam[2]],
        [y_cam[0], y_cam[1], y_cam[2]],
        [z_cam[0], z_cam[1], z_cam[2]]
    ])

    # A translação é o negativo do produto escalar da posição da câmera com cada eixo da câmera.
    # Ou, mais simples, -matriz_rotacao @ posicao_camera
    matriz_translacao = -matriz_rotacao @ posicao_camera

    # Montando a Matriz de Visualização (View Matrix) 4x4
    matriz_visualizacao = np.eye(4)
    matriz_visualizacao[:3, :3] = matriz_rotacao
    matriz_visualizacao[:3, 3] = matriz_translacao
    return matriz_visualizacao

# Exemplo de uso:
pos_cam = np.array([5.0, 3.0, 10.0])
pos_alvo = np.array([0.0, 0.0, 0.0])
up_mundo = np.array([0.0, 1.0, 0.0])

matriz_view = look_at(pos_cam, pos_alvo, up_mundo)
print("Matriz de Visualização (Look-At):\n", matriz_view)

Implementando a C​âmera Orbital

​Para uma câmera orbital, calculamos a posição da câmera com base em ângulos (azimute, elevação) e uma distância do alvo, e então usamos a função look_at.

def calcular_posicao_orbital(posicao_alvo, distancia, angulo_azimute_rad, angulo_elevacao_rad):
    # Coordenadas esféricas para cartesianas
    x = posicao_alvo[0] + distancia * np.cos(angulo_elevacao_rad) * np.sin(angulo_azimute_rad)
    y = posicao_alvo[1] + distancia * np.sin(angulo_elevacao_rad)
    z = posicao_alvo[2] + distancia * np.cos(angulo_elevacao_rad) * np.cos(angulo_azimute_rad)
    return np.array([x, y, z])

# Exemplo de câmera orbital:
distancia_orbital = 15.0
azimute_graus = 45.0
elevacao_graus = 30.0

pos_cam_orbital = calcular_posicao_orbital(
    pos_alvo,
    distancia_orbital,
    np.radians(azimute_graus),
    np.radians(elevacao_graus)
)

matriz_view_orbital = look_at(pos_cam_orbital, pos_alvo, up_mundo)
print(f"\nPosição da Câmera Orbital: {pos_cam_orbital}")
print("Matriz de Visualização Orbital:\n", matriz_view_orbital)

Matriz de Projeção Perspectiva

​Finalmente, a matriz de projeção transforma o espaço da câmera para o espaço de recorte.

def criar_matriz_projecao_perspectiva(fov_rad, aspect_ratio, near, far):
    f = 1.0 / np.tan(fov_rad / 2.0)
    matriz_projecao = np.zeros((4, 4))
    matriz_projecao[0, 0] = f / aspect_ratio
    matriz_projecao[1, 1] = f
    matriz_projecao[2, 2] = (far + near) / (near - far) # Mapeia Z para [-1, 1] se z_cam estiver em [-near, -far]
    matriz_projecao[2, 3] = (2 * far * near) / (near - far)
    matriz_projecao[3, 2] = -1.0 # Coloca -z_cam em w
    return matriz_projecao

# Exemplo de Projeção:
fov_graus = 60.0
aspecto = 16.0 / 9.0
plano_proximo = 0.1
plano_distante = 100.0

matriz_proj = criar_matriz_projecao_perspectiva(np.radians(fov_graus), aspecto, plano_proximo, plano_distante)
print("\nMatriz de Projeção Perspectiva:\n", matriz_proj)

Aplicando as Transformações

Para transformar um vértice (ponto) do espaço do modelo para o espaço de tela (antes da divisão por W e mapeamento de viewport):

# Vértice no espaço do modelo (coordenadas homogêneas)
vertice_modelo = np.array([1.0, 0.5, 2.0, 1.0])

# Matriz de Modelo (exemplo: identidade, sem transformação de modelo)
matriz_modelo = np.eye(4)

# MVP Matrix
matriz_mvp = matriz_proj @ matriz_view @ matriz_modelo

# Vértice transformado para o espaço de recorte
vertice_recorte = matriz_mvp @ vertice_modelo
print("\nVértice no Espaço do Modelo:", vertice_modelo)
print("Vértice no Espaço de Recorte (antes da divisão por W):", vertice_recorte)

# Divisão Perspectiva (dividir por W)
if vertice_recorte[3] != 0:
    vertice_ndc = vertice_recorte / vertice_recorte[3]
    print("Vértice em Coordenadas Normalizadas de Dispositivo (NDC):", vertice_ndc)

​Esses exemplos fornecem a base computacional para as transformações. Em uma aplicação gráfica real, esses cálculos seriam feitos para cada vértice de cada objeto na cena, a cada quadro, e o resultado seria usado para renderizar a imagem na tela, geralmente com o auxílio de APIs gráficas como OpenGL ou DirectX, que são otimizadas para essas operações.
Se formos abordar esse assunto a fundo, escreveriamos livros aqui, e não apenas um artigo. é isso!